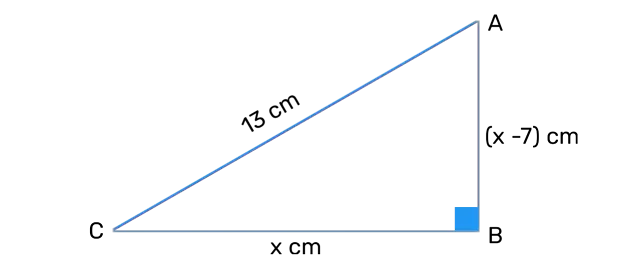
Ex 4.2 Q5 - The altitude of a right triangle is 7 cm less than its base

Ex 4.2 Q5 - The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.

Solution:-

Given,

      Hypotenuse = 13 cm

Let,

      Base = 'x' cm

➙ As it is given that the altitude of triangle is 7 cm less than its base,

   ∴ Altitude = (x - 7) cm

➙ Using Pythagoras theorem,

      (Hypotenuse)² = (Base)² + (Altitude)²

   ∴ (13)² = (x)² + (x - 7)²

   ∴ 169 = x² + x² - 14x + 49

   ∴ 169 = 2x² - 14x + 49

   ∴ 2x² - 14x + 49 - 169 = 0

   ∴ 2x² - 14x - 120 = 0

   *Taking 2 as common

   ∴ x² - 7x - 60 = 0

*Although you can use any method for solving this quadratic equation i.e Factorization method, Completing the square method, or Quadratic formula.

Here we'll use Factorization method as it is very easy and less time consuming..

   ∴ x² - 7x - 60 = 0

   ∴ x² - 12x + 5x - 60 = 0

   ∴ x(x - 12) + 5(x - 12) = 0

   ∴ (x - 12) (x + 5) = 0

Now,

      x - 12 = 0           OR           x + 5

   ∴ x = 12                              ∴ x = -5

But, x can't be negetive as it is a side of triangle,

   ∴ x = 12

Therefore,

   *Base = x = 12 cm

   *Altitude = x - 7

                     = 12 - 7

                     = 5 cm

Hence,

         The other two sides of the triangle are 12 cm (Base) and 5 cm (Altitude).

------------------------------------

Try This..

✒ The hypotenuse of a right triangle is 10 cm more than the base. If the height is 24 cm, find the base and hypotenuse.

✒ The difference between the hypotenuse and a side of a right triangle is 1 cm. If the other side is 7 cm, find the sides of the triangle.

✒ A ladder is placed against a wall. The foot of the ladder is 9 m away from the wall and the ladder reaches a height of 12 m. Find the length of the ladder.

❌ Common Mistakes

Incorrectly Forming the Equation:

▸ Many students wrongly assume the base or height or forget the “7 cm less” condition.

Wrong Application of the Pythagoras Theorem:

▸ Some write; Hypotenuse² = Base – Height², which is incorrect.

Forgetting to Simplify the Quadratic Equation:

▸ Students often forget to reduce the equation in its simplest form.

Accepting Negative Root:

▸ Discard the negative roots as length can't be negetive.

📝 Related Questions:-

• Ex 4.2 Q6 - A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was ₹90, find the number of articles produced and the cost of each article.
• Ex 4.2 Q4 - Find two consecutive positive integers, sum of whose squares is 365.

Queries Solved:-

Class 10 Ex 4.2

Ex 4.2 Q5 Class 10

Class 10 Ex 4.2 Q5

Class 10 Chap 4 Ex 4.2 Q5

Class 10 Quadratic Equations

If you found it helpful, please leave a comment below sharing your thoughts or questions. 

Don’t forget to share it with your classmates to help them learn too. 

Good luck, and happy learning!

Together, let’s make math simpler and more enjoyable for everyone!