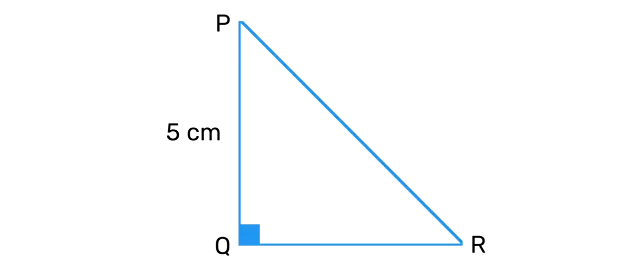
Ex 8.1 Q10 - In ∆PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sinP, cosP and tanP.
Solution:-Given,
PQ = 5 cm
PR + QR = 25 cm
∴ PR = 25 -QR ----- (1)
➙ Applying Pythagoras theorem in ∆PQR,
(Hypotenuse)² = (Base)² + (Altitude)²
∴ PR² = QR² + PQ²
∴ (25 - QR)² = QR² + (5)² -- from Eqⁿ(1)
∴ 625 - 50QR + QR² = 25 + QR²
∴ 50QR = 625 - 25
∴ 50QR = 600
∴ QR =
600
/
50
∴ QR = 12 cm
➙ Putting QR = 12 in Eqⁿ(1)
∴ PR = 25 - 12
∴ PR = 13 cm
Now,
*sinP =
Opposite side of ∠P
/
Hypotenuse
=
QR
/
PR
=
12
/
13
∴ sinP =
12
/
13
*cosP =
Adjacent side of ∠P
/
Hypotenuse
=
PQ
/
PR
=
5
/
13
∴ cosP =
5
/
13
*tanP =
Opposite side of ∠P
/
Adjacent side of ∠P
=
QR
/
PR
=
12
/
5
∴ tanP =
12
/
5
Alternatively,
*tanP =
sinP
/
cosP
=
12/13
/
5/13
=
12
/
5
∴ tanP =
12
/
5
Hence,
The values of sinP, cosP and tanP are 12/13, 5/13 and 12/5 respectively.
------------------------------------
Try This..
✒ In triangle PQR, right-angled at Q, if PQ = 8 cm and the difference between PR and QR is 6 cm, calculate sin P, cos P, and tan P.
✒ A triangle XYZ is right-angled at Y. If XY = 7 cm and XZ – YZ = 11 cm, find the trigonometric ratios of angle X.
✒ In triangle ABC, right-angled at B, if AB = 9 cm and the sum of sides AC and BC is 30 cm, find sin A, cos A, and tan A.
❌ Common Mistakes
Misidentifying sides:▸ Always label opposite, adjacent, and hypotenuse correctly based on the reference angle.Incorrect substitution:▸ Plugging in wrong values in Pythagoras’ Theorem or forgetting to square the terms.Skipping verification:▸ Always double-check that your triangle satisfies the Pythagorean identity.
Queries Solved:-
Class 10 Ex 8.1
Ex 8.1 Q10 Class 10
Class 10 Ex 8.1 Q10
Class 10 Chap 8 Ex 8.1 Q10
Class 10 Introduction To Trigonometry
If you found it helpful, please leave a comment below sharing your thoughts or questions.
Don’t forget to share it with your classmates to help them learn too.
Good luck, and happy learning!
Together, let’s make math simpler and more enjoyable for everyone!