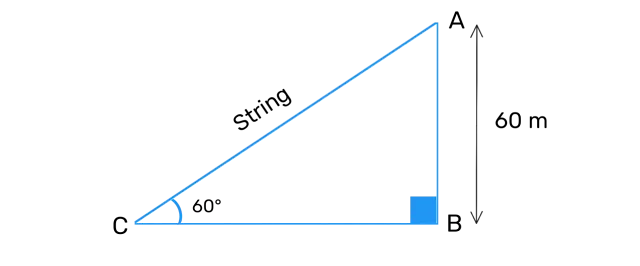
Ex 9.1 Q5 - A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Solution:- *AB be the height of flying kite
*AC be the length of the string
which is tied at point C
Given,
*Height of flying kite = AB = 60 m
*Inclination of string with the ground
= ∠ACB = 60°
➙ In ∆ABC, ∠ABC = 90°,
∴ sinC =
Opposite side of ∠C
/
Hypotenuse
∴ sin60° =
AB
/
AC
∴ sin60° =
60
/
AC
{ Given } ∴
√3
/
2
=
60
/
AC
{ ∵ sin60° = √3/2 } ∴ AC =
60 × 2
/
√3
*Multiplying Numerator and Denominator by √3
∴ AC =
60 × 2
/
√3
×
√3
/
√3
∴ AC =
60 × 2 × √3
/
3
∴ AC = 40√3
Hence,
The length of the string is 40√3 m.
------------------------------------
Try This..
✒ A tower is 100 m tall. A guy wire is attached from the top to the ground at a 45° angle. Find the length of the wire.
✒ A man on the ground sees a bird on a tree at an angle of elevation of 45°. The height of the tree is 20 m. Find the distance of the bird from the man.
✒ A balloon is flying at a height of 50 m. The angle of elevation from a point on the ground is 30°. Find the length of the string.
❌ Common Mistakes
Confusing the trigonometric ratios:▸ Remember, sin = opposite/hypotenuse, cos = adjacent/hypotenuse, and tan = opposite/adjacent.Using the wrong angle:▸ Always match the sides correctly with the given angle.Not rationalizing the denominator:▸ Many forget to rationalize when the answer has a square root in the denominator.Incorrect value of trigonometric ratios:▸ Memorize standard values like sin 30°, sin 60°, etc.
📝 Related Questions:-
- Ex 9.1 Q1 - A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.
- Ex 9.1 Q2 - A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
- Ex 9.1 Q3 - A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
- Ex 9.1 Q4 - The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
- Ex 9.1 Q8 - A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Queries Solved:-
Class 10 Ex 9.1
Ex 9.1 Q5 Class 10
Class 10 Ex 9.1 Q5
Class 10 Chap 9 Ex 9.1 Q5
Class 10 Some Applications Of Trigonometry
If you found it helpful, please leave a comment below sharing your thoughts or questions.
Don’t forget to share it with your classmates to help them learn too.
Good luck, and happy learning!
Together, let’s make math simpler and more enjoyable for everyone!